iGEM中的常微分方程模型

根据笔者去年参加iGEM的经验，整理得到本文，供后面参加iGEM并负责建模的同学参考。

本文中建模使用的编程语言是MATLAB。

Logistic方程

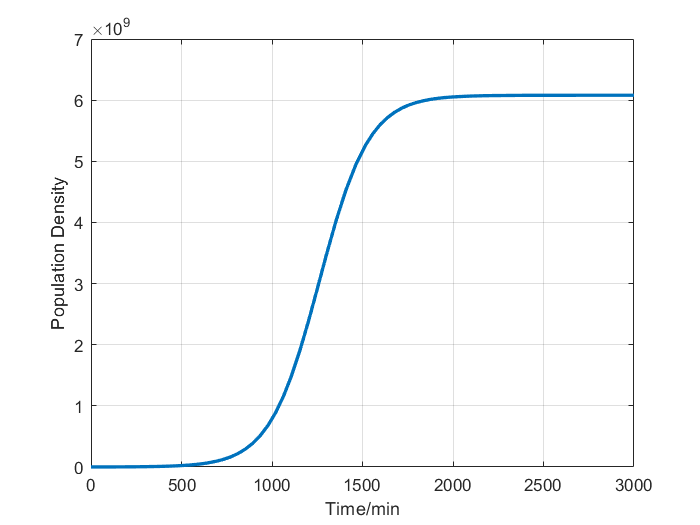
Logistic方程可以用于种群动力学模型的建模。设$N$是某种生物的种群密度，则 $${\displaystyle \frac{\mathrm{d}N}{\mathrm{d}t}}=rN\cdot (1-{\displaystyle \frac{N}{K}}),$$ 其中$r$是生长率，$K$是环境容纳量。该方程可以求出解析解 $$N(t)={\displaystyle \frac{K{N}_0\cdot {\mathrm{e}}^{rt}}{K+N_0\cdot ({\mathrm{e}}^{rt}-1)}},$$ 其中$N_0=N(0)$是初始数量。该方程可以应用于：

• 给定生长率$r$和环境容纳量$K$，预测种群数量的变化，需要使用ode45函数。
• 给定种群数量随时间变化的数据，计算生长率并预测种群的最大数量，需要使用lsqcurvefit函数。

物质守恒定律

所谓的物质守恒定律，说的是物质不会凭空消失，也不会凭空产生，只能由一种物质转化成另一种物质。在物质的转化过程中，就需要用到该定律。

以中心法则为例，DNA首先转录为RNA，再由RNA翻译为蛋白质，这个过程就涉及到了物质的转化。

设蛋白质$x$的生产由启动子$A$决定，其浓度为$[x]$，对应的DNA浓度恒定且为$[dx]$，RNA浓度为$[rx]$。对于转录的过程，有 $${\displaystyle \frac{\mathrm{d}[rx]}{\mathrm{d}t}}=k_{syn,x}\cdot {\alpha }_A\cdot [dx]-k_{de,x}\cdot [rx],$$ 其中$k_{syn,x}$是$x$对应的RNA转录速率，$k_{de,x}$是$x$对应的RNA降解速率，${\alpha }_A$是启动子$A$的表达率，如果$A$受到其他因素的影响，可以将其写成${\alpha }_A={\alpha }_{A,0}+{\alpha }_{A,i}$，其中${\alpha }_{A,0}$是$A$的本底表达率，${\alpha }_{A,i}$是$A$的诱导表达率。对于翻译的过程，有 $${\displaystyle \frac{\mathrm{d}[x]}{\mathrm{d}t}}=k_{psyn,x}\cdot [rx]-k_{pde,x}\cdot [x],$$ 其中$k_{psyn,x}$是$x$的翻译速率，$k_{pde,x}$是$x$的降解速率。该定律可以应用于预测RNA和蛋白质的产量，需要对微分方程组使用ode45函数。

Michaelis-Menten方程

Michaelis-Menten方程是表示一个酶促反应的起始速度与底物浓度关系的速度方程。

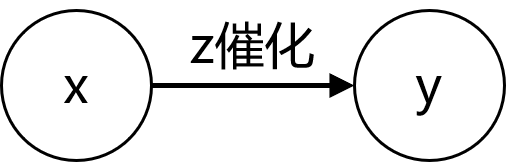
设蛋白质$x$转化成蛋白质$y$的过程由蛋白质$z$催化，并设它们的浓度分别为$[x]$、$[y]$和$[z]$，则有 $${\displaystyle \frac{\mathrm{d}[y]}{\mathrm{d}t}}={\displaystyle \frac{v_{max,z}\cdot [x]}{[x]+k_{m,z}}},$$ 其中$v_{max,z}=k_{cat,z}\cdot [z]$，$k_{cat,z}$是$z$的催化效率，$k_{m,z}$是常数。该方程可以用于预测蛋白质的产量，需要使用ode45函数。

建模主要的工作是模拟和预测，并根据结果来给出建议。要了解更多，可以参考2021年的建模结果：Team:XJTU-China/Model。